Skip to main content

Mixnet Routing

Routing of messages on Quilibrium's network utilizes a mixnet approach called RPM, in which each logical cluster (clique) permutes the messages following a threshold permutation matrix scheme.

Basics

Mixnets at a simplified point of view can be thought of as a black box that takes in messages from senders, and relays them to recievers, such that an attacker with access to info outside this black box (but not within) cannot correlate the sender to the recipient. While mixnets have been around for a long time, the research on deanonymizing users has also vastly expanded in scope, and so advanced techniques have been developed to help preserve anonymity of users. The threat model can be summarized as the following types of attackers:

  • External, Active – the attacker introduces their own traffic to the mixnet to enhance the analysis of traffic flow, or disrupt operations to better identify individuals.
  • External, Passive – the attacker monitors traffic to and from the mixnet operators, and the exact timings of communication that occurred.
  • Internal, Active – the attacker operates as a malicious mixnet node to actively drop some amounts of traffic to distinctively identify individuals.
  • Internal, Passive – the attacker operates as a normal mixnet node to decrypt one or more hops of the traffic.

Our approach to solving these problems is through economic disincentives making it too expensive to broadly interrupt traffic flow at the external active attacker level, our direct routing strategy through RPM detailed further below to completely make the internal active/passive attacker models fail, as they would identify the bad actor through protocol aborts, and finally through our gossip layer BlossomSub to make the external passive model infeasible.

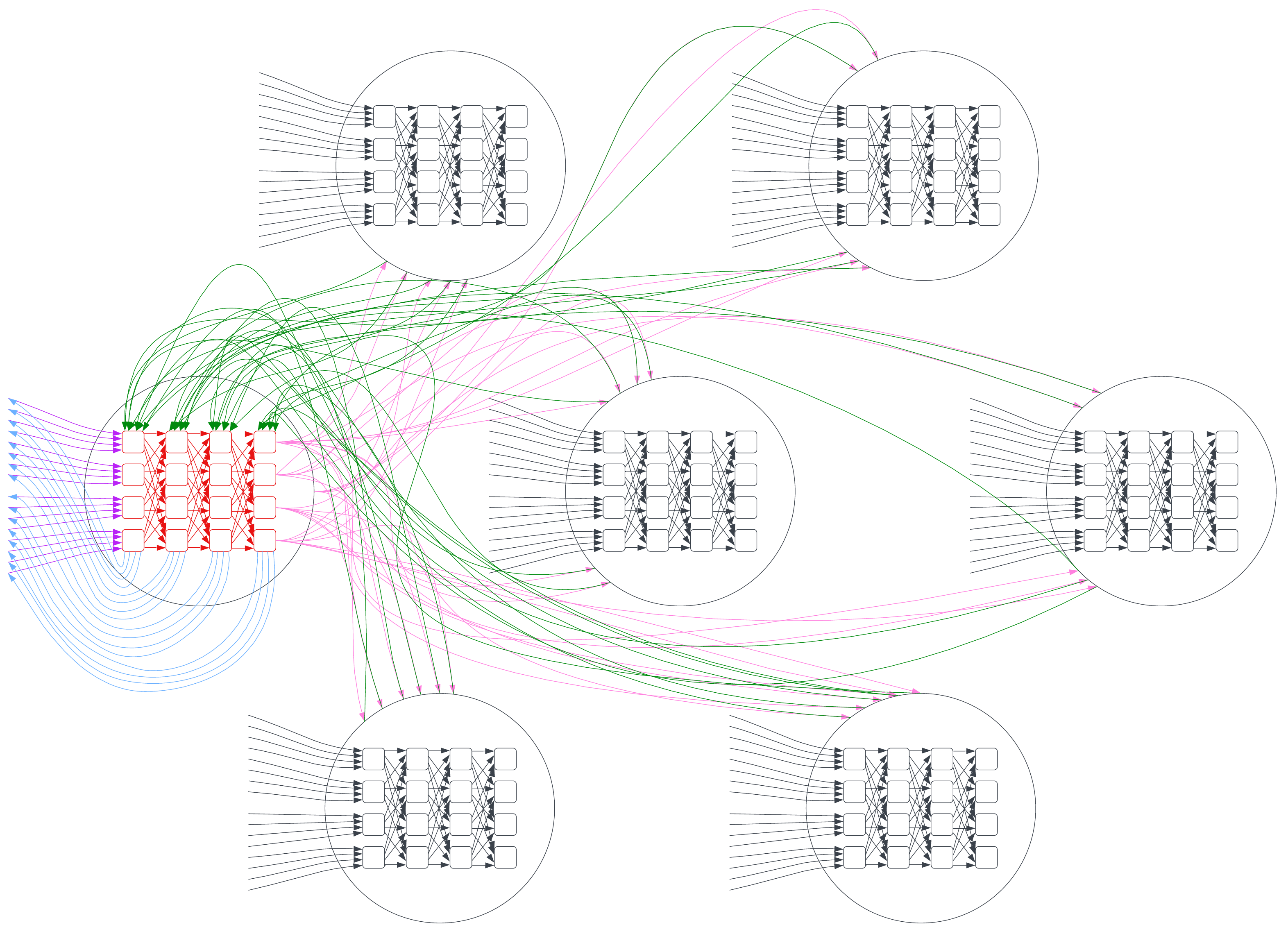
RPM

Focusing strictly on the raw details of RPM before expanding to the full utilization on the network, RPM works through a technique of building a collection of random permutation matrix secret shares, along with Beaver triples in an offline process, then collecting input messages for distribution as secret-shared blocks from the senders, and collectively across the span of nodes participating, perform Shamir recombination and multiplication of the input vector through the MPC-derived permutation matrix, resulting in an output vector of messages which have no meaningful correlation to the originating sender that can be derived by any participant. To enhance the scalability of this process, instead of one large permutation matrix, smaller permutation matrices are generated and then arranged in a square lattice network, following the Square Lattice Shuffle technique.

A Deeper Dive

The RPM protocol follows three phases in its direct implementation, however we augment it with an additional process recommended in the paper for a matched request/response scheme, resulting in five phases:

  1. Message Collection
  2. Server Permutation
  3. Broadcast
  4. Processing/Acknowledgement
  5. Transpose Mix

To give a visual understanding of this process in the scope of a logical clique (cluster), click the phases in the diagram below:

All Phases ▶ Message Collection ▶ Server Permutation ▶ Broadcast ▶ Processing/Acknowledgement ▶ Transpose Mix

Message Collection

The preparation at the client level requires the creation of a Shamir split of the message m, that can be ordered deterministically by the servers. This is achieved by generating Shamir shares of a random value r given out to the client, recombined by the client, and added to the message m + r, blinding it. This message can be sent to the servers, who can subtract their share of r and collectively recombine it in the permutation phase to find m.

Server Permutation

The permutation process is performed with the input vector of blinded messages Y = P · (X + R) − PR. This results in an output vector Y of unblinded messages, in completely shuffled order.

Calculation of a permutation matrix through a series of secret sharings first requires the calculation of a Beaver multiplication triple to perform multiplication (denoted as Mul(x, y)):

Offline Calculation of Permutation Matrix Sharings:
  1. All parties generate a k × k permutation matrix Mi and generates secret sharings, distributing to each party
  2. All parties verify the columns and rows of each sharing using sketch checks to verify the sharings correspond to a valid permutation matrix, aborting if a check fails.
  3. All parties multiply their received matrix shares and their own share of their matrix, ⟨P⟩ = ⟨M1⟩⟨M2⟩...⟨Mn⟩
  4. All parties generate k random shares, producing the vector ⟨R⟩ = {⟨r1⟩,⟨r2⟩, ...,⟨rk⟩}
  5. All parties compute ⟨P R⟩, = Mul(⟨P⟩,⟨R⟩)

The online combination phase follows:

Online Matrix Permutation Recombination:
  1. All parties receive blinded messages using chosen random shares, and are slotted into matching positions of the R vector
  2. All parties recombine the input vector, yielding X + R.
  3. All parties calculate ⟨Y⟩ = ⟨P⟩ · (X + R) − ⟨PR⟩, and then recombine to produce Y.

Broadcast

All messages are broadcast, to be retrieved by their intended recipients, following BlossomSub.

Processing/Acknowledgement

Messages are confirmed to destination, acknowledgement message is returned.

Transpose Mix

The transpose of the permutation matrix shares is followed of the tagged acknowledgements, producing clean acknowledgements in the same order as client requests, allowing anonymous retrieval of confirmation.