E2EE

End-to-End Encryption (E2EE) is a critical component in ensuring communication between nodes is secured, but E2EE can mean many things. For the purpose of Quilibrium, we employ an E2EE scheme that retains forward and future secrecy properties, called Triple-Ratchet.

Basics

E2EE, simply stated, is an encryption scheme that ensures the individual parties in communication with one another are the only individuals that can ever see the plaintext. When thinking about what constitutes E2EE, it's important to think of "parties" as not just people, but systems. Thus, if a conversation between Alice and Bob is E2EE, no systems or intermediaries that facilitate that conversation have the ability to read their messages. There are many approaches to E2EE, with tradeoffs to performance, security and secrecy.

In terms of some of those tradeoffs, we want to have the following properties:

Forward Secrecy – that if a key used in the encryption of a conversation is obtained by an attacker, previous messages are still not decryptable by the attacker.
Post-Compromise Secrecy – that if a key used in the encryption of a conversation is obtained by an attacker, messages created after the compromise has been ended are still not decryptable by the attacker.
Repudiability – that the algorithmic approach to securing the conversation is done such that once messages have been sent/received, it is impossible to know from the data after the event that they truly were originated by the author, granting the author plausible deniability to any message that they have written.
Replay Protection – that messages that are re-sent do not result in duplicate messages or potential confusion of the current state of keys used to secure the system.
Out-of-Order Messaging – that networks/systems may reorder messages, but the recipients will still be able to produce the correct sequence as intended by the author, and tolerate those incorrect sequences without losing security.

To start constructing an approach, let's consider a few tools we can utilize.

ECDH

Elliptic Curve Diffie-Hellman (ECDH) is a key agreement protocol in which two parties exchange elliptic public keys (P and Q), and using the commutative properties of scalar multiplication of elliptic curve points,

p * Q = p * q * G = q * p * G = q * P

and thus both parties can agree to a shared value others cannot deduce, as others do not possess either parties' private key scalar. Let's walk through a protocol that uses only ECDH and assess what properties it provides:

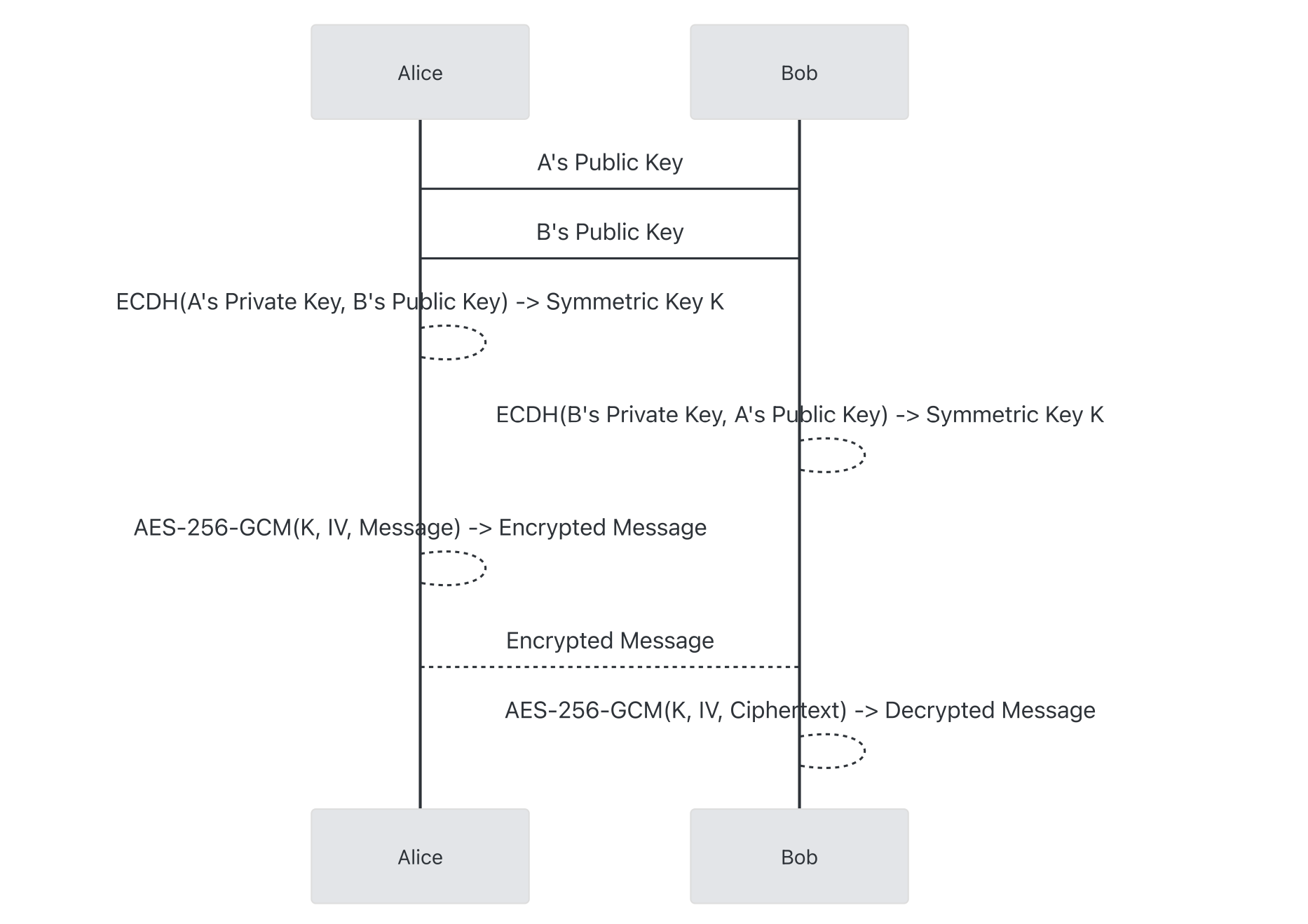
In this simple example both parties agree to a singular symmetric key via ECDH. Let's revisit our desired properties – does this approach have these?

🚫 Forward Secrecy – Since there is only one key, if compromised, all previous messages are decryptable.
🚫 Post-Compromise Secrecy – Likewise, all future messages are also decryptable.
✅ Repudiability – Because there is only one key that both parties have access to, only the sender and receiver can know who truly originated the message, or if it was even authentically their own.
🚫 Replay Protection – This approach does not prevent replays, as the message content sent is indistinguishable from an intentional duplicate.
🚫 Out-of-Order Messaging – This approach does not prevent out-of-order messaging, as there is no way to algorithmically distinguish whether one message precedes the other.

danger

There is also one other element to consider – interdiction. If an attacker were to insert them in the middle of this channel and pairwise establish ECDH with each side, they could pretend to be the other party, or silently pass messages while being able to read them. There is a way to prevent this by deriving a value from the agreed key and allowing both sides to confirm out of band, but this will vary by approach and so for now, we omit this consideration beyond noting its existence.

ECDH Ratcheting

Let's augment this with an intermediate step: every time the first message is received from the other party after having sent our own messages, create a new public key, and perform ECDH with their public key. When sending a message back, include our new public key so they can decrypt. On their turn of first receipt, they will also create a new public key for their next send, thus ratcheting both sides over alternating intervals. What does this net us?

✅ Forward Secrecy – Since there is a new key every alternating round, if a key is compromised, previous messages are not decryptable.
✅ Post-Compromise Secrecy – Likewise, future messages post ratchet are also not decryptable.
✅ Repudiability – Because both parties have access to the same symmetric keys, only the sender and receiver can know who truly originated the message.
🚫 Replay Protection – This approach does not prevent replays, as the message content sent is still indistinguishable from an intentional duplicate.
🚫 Out-of-Order Messaging – This approach slightly prevents out-of-order messaging, in that we can ensure sender and receiver ordering is correct, but not within the scope of a sender or receiver.

So we're almost there. How can we gain those last two properties?

KDF Ratcheting

The KDF ratchet employs the use of a hash-based message authentication code (HMAC). A common HMAC in this scenario is HMAC-SHA256. As a function, you can consider HMAC defined generally as

HMAC(K, m) = H((K' xor opad) || H((K' xor ipad) || m)

To break this down into what this means and why, let’s first label the pieces.

H(x) – a hash function.
K – the secret key.
m – the message.
opad – the outer padding, consisting of the byte 0x5C repeated for the byte length of the block.
ipad – the inner padding, consisting of the byte 0x36 repeated for the byte length of the block.
K' – a derivation of K, where when smaller than the block size is padded to the right with zeroes to the byte length of the block, or hashed with H to either less than or equal to the block size and padded to the right with zeroes if shorter.

This produces an output sized to the hash function. HMAC, in conjunction with an expansion function, creates a secure KDF with definable length. We can describe this function as HKDF(salt, K, m, L). The two additional elements here are salt, a non-secret random value or a byte string of zeroes to the length of the hash function, and L, the length of the KDF output in bytes. The process for the HKDF has two phases: an extract phase, which is just the invocation of the HMAC as HMAC(salt, K) (note the order), and using that value as a pseudo-random key PRK in the expand phase, which can be expressed in the following pseudocode:

int hl = <length_of_hash_function_in_bytes>int n = (L / hl) + (L % hl > 0 ? 1 : 0)string t = "" for (byte i = 0x01; i <= n; i++) { // assume + is a concatenation operator here: t = HMAC(PRK, t + m + i)} return t[0..n]

We can now take this KDF and chain it with itself, using the output length in bytes to produce a block that can be split into constituent pieces as needed, at a minimum the same length as the input key, to be fed back into the KDF. This will get used in conjunction with the Diffie-Hellman Ratchet to produce the Double-Ratchet algorithm. Because the iterations of KDF ratcheting produces a deterministic key sequence, we have now obtained guaranteed uniqueness for messages (replay protection) and message ordering (no out-of-order messages). This provides a highly-secure two-party E2EE scheme, but how do we handle groups of any count?

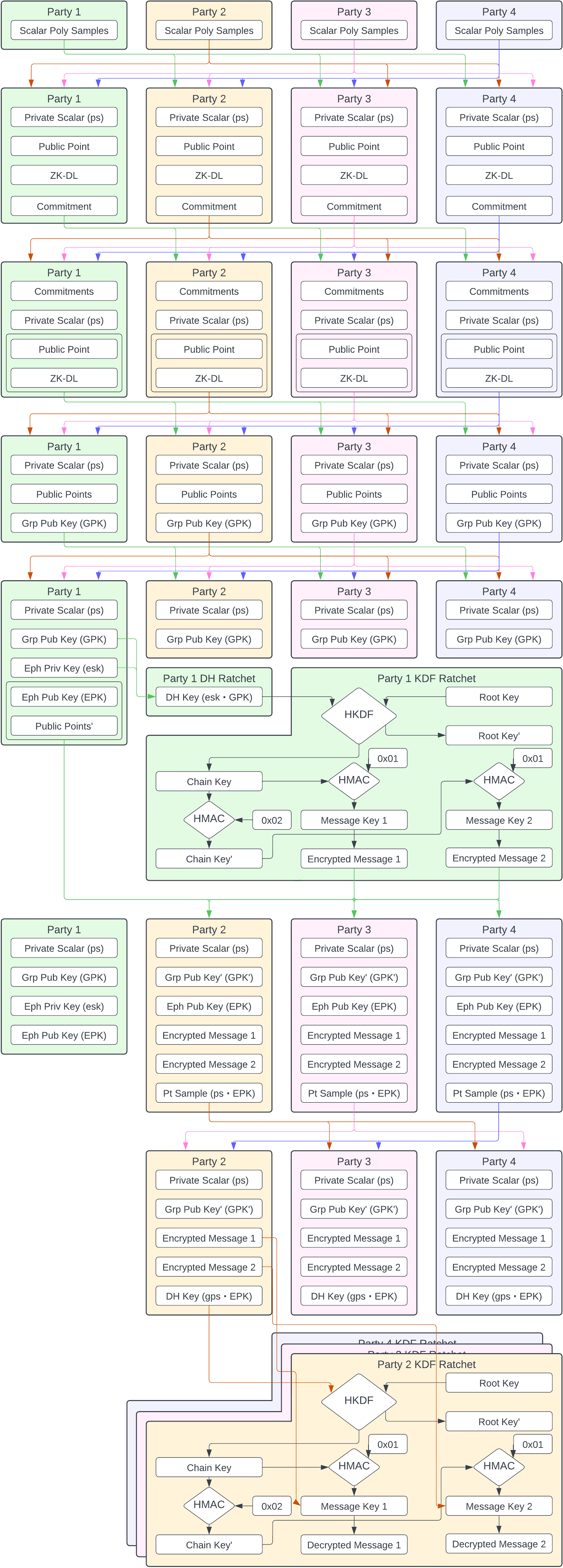
Triple-Ratchet

The Triple-Ratchet protocol is an extension to the Double-Ratchet protocol, utilizing an asynchronous DKG ratchet (or synchronous DKG ratchet in a fully-online model, not applicable here) to provide a “room key” as the counterparty receiver key plugged into the Double-Ratchet algorithm’s Diffie-Hellman process. This DKG ratchet can be broken down into three rounds:

Polynomial Sampling
Point Calculation, Proof Construction and Commitment Distribution
Point and Proof Distribution, Reconstruction

Polynomial Sampling

Shamir’s Secret Sharing is a technique for encoding a secret in the form of a constant of a randomly sampled polynomial, then distributing evaluations of that polynomial to each participant such that the threshold number of participants in the scheme could perform Lagrange interpolation to reproduce the constant:

Given a threshold of three participants, construct a $t-1$ degree polynomial, randomly sampling coefficients ($A, B$) from the finite field, setting the constant $C$ as the secret:

f(x) = Ax²+Bx+C

The dealer of these secret shares then evaluates the polynomial where x is the identifier of the participant (notably, x cannot equal zero as it would simply be handing the participant the secret, and likewise, x cannot be the order of the group either, as x mod q = 0 where x = q.

The dealer distributes these samples to each participant, and when recombining, the participants calculate:

C = f(0) =

t-1

j=0

y_j

t-1

(m=0)

m!=j

x_m

x_m - x_j

Shamir Secret Sharing's downside is, used directly, it only works with a known secret value, which would mean one party would have to be trusted. Thus, we have to augment this approach such that we can verify the shares are valid for all parties, and that no one party has to be trusted. To solve the first problem, Feldman Verifiable Secret Sharing (FVSS) brings the same premise, but with a verifiable proof.

Solving the second problem, the need for a trusted dealer, simply have all parties perform FVSS and distribute polynomial samples, then calculate your local share by adding your received samples to your secret.

Point Calculation, Proof Construction and Commitment Distribution

Following the group polynomial sampling, once all parties have received their samples and added them to their secret values, to calculate the verifiable aspect of FVSS, take the local secret as a scalar to the generator of the curve s * G = P.

Before distributing P to everyone, we instead calculate a zero knowledge proof that we possess the scalar corresponding to P, then present a commitment to that proof:

Generate a new random scalar, r_i, and its corresponding public point R_i = r_i * G, matching the same curve parameters as the mutually agreed key.
To make this process non-interactive, we will apply the Fiat-Shamir heuristic by hashing the serialized threshold sharing’s public key concatenated with the random public point: ch_i = H(P_i||R_i)
To calculate the ZKPoK, we take the threshold secret, multiply it against the integer representation of the challenge, and add the random scalar: z_i = s_i * ch_i + r_i
We finally commit to this ZKPoK by taking the hash of the serialized random public point concatenated with the ZKPoK: c_i = H(R_i||z_i)
This commitment is to be broadcast ahead of the sharing of the public points.

Point and Proof Distribution, Reconstruction

Once all parties have broadcasted their commitments, distribute P_i, z_i, and R_i. With these values, verify:

Reproduce the challenge by hashing the concatenation of the serialized threshold sharing’s public key with the random public point: ch_j = H(P_j||R_j)
Multiply the challenge scalar against the threshold sharing public key, then add the random public point to this point, which should equal the scalar multiplication of the ZKPoK against the generator of the curve: Z_j = ch_j * PK_j + R_j
Multiply the ZKPoK against the generator of the curve and confirm this value equals the previously calculated value, and abort if this does not match: z_j * G = Z_j
Take the hash of the serialized random public point concatenated with the ZKPoK, and confirm this matches the commitment, and abort if this does not match: c_j = H(R_j||z_j)
If the values matched, verification has succeeded.

Finally, all participants may do Lagrange interpolation of the polynomial with the public values of the shares (Shamir in the Exponent), iterating through all participants. The resulting output, provided no party cheated, will equal P for all combinations of threshold participants. If someone did cheat, some or all of the combinations will not equal P.

ADKG Ratchet

Now that we have a means to ensure no party can produce invalid fragments, we can adopt a new ratcheting scheme for DKG. Each party will (upon their need to ratchet):

Individually perform a local FVSS with PVS, and enqueue the output bundles to the respective recipients.
When a new bundle is needed from a given party, the other participants will dequeue the bundle, and perform the verification process of PVS. Upon confirmation of verification, each party will recalculate the new shared polynomial, substituting the old fragment with the new to obtain a new s_i, and each party will send their public point P_i.
Each party then performs FVSS’ Shamir-in-the-Exponent recombination of the public points.

To perform Diffie-Hellman over this distributed key, swap the generator point with the other party's public key and perform the above DKG process. To visually summarize, here is an example of the entire Triple-Ratchet algorithm exchange, in a 3-of-4 threshold configuration: